Qué define a una función sobreyectiva y ejemplos

• Las funciones sobreyectivas establecen un puente transparente y eficiente entre conjuntos de entrada y salida, al garantizar que cada elemento del conjunto meta encuentre, al menos, un correspondiente en el conjunto de origen.
• Este concepto es crucial para simplificar la resolución de complejas ecuaciones matemáticas, proporcionando una estructura bien definida que facilita tanto su análisis como su comprensión.
• Al explorar sus criterios, contrastes con otras funciones, ejemplos concretos y aplicaciones prácticas, se resalta su importancia en diversas áreas de estudio.
• Además, se abordan métodos efectivos para su identificación y se discuten los desafíos encontrados, siempre buscando clarificar su comprensión y manejo.

Adentrarse en el mundo de las matemáticas es sumergirse en un océano de conceptos, teorías y aplicaciones prácticas que moldean nuestra comprensión del universo. Entre estos conceptos, las funciones sobreyectivas destacan por su rol fundamental en las estructuras matemáticas y su aplicabilidad en diversos campos.

Este artículo despliega un análisis exhaustivo sobre las funciones sobreyectivas, desde su definición hasta ejemplos prácticos, revelando su importancia y cómo identificarlas. Prepárate para una inmersión profunda en esta fascinante temática que, sin duda, enriquecerá tu comprensión matemática.

Definición de función sobreyectiva

Criterios para la sobreyección

En el corazón de la definición de una función sobreyectiva yacen ciertos criterios que la distinguen de otros tipos de funciones. Primordialmente, una función es sobreyectiva si, y solo si, cada elemento del conjunto de salida (codominio) tiene al menos un elemento correspondiente en el conjunto de entrada (dominio). En otras palabras, la función cubre completamente su codominio, no dejando ningún "punto" sin mapear.

Comparación con otros tipos de funciones

Distinguir entre funciones injectivas, sobreyectivas y biyectivas es crucial para una comprensión completa. Mientras las funciones injectivas aseguran que no haya dos elementos diferentes del dominio apuntando al mismo elemento del codominio, una función biyectiva cumple con ser al mismo tiempo injectiva y sobreyectiva. El distinguir entre estas permite entender cómo las sobreyectivas aseguran una cobertura total del codominio.

Ejemplos de funciones sobreyectivas

Funciones lineales sobreyectivas

Un ejemplo clásico de función sobreyectiva es la función lineal [f(x) = mx + b], donde [m] y [b] son constantes, y [m neq 0]. Aquí, el conjunto de todos los valores reales que x puede tomar se mapean uniformemente a través del conjunto de valores reales de y, asegurando que la función sea sobreyectiva. Esta simplicidad y elegancia hacen de las funciones lineales herramientas poderosas.

Funciones polinomiales y su sobreyección

Las funciones polinomiales también ofrecen fascinantes ejemplos de sobreyección, especialmente aquellas de grado impar. Piénsese en [f(x) = x^{3}], cuya curva continua y su comportamiento a nivel infinito aseguran que cada posible valor en y tenga al menos un valor en x que lo origine, evidenciando su sobreyección.

Importancia de las funciones sobreyectivas

Aplicaciones en matemáticas

La relevancia de las funciones sobreyectivas en matemáticas es innegable. Facilitan la comprensión de conceptos como la inversión de funciones y la teoría de conjuntos, jugando un rol crucial en el análisis y en la topología al proveer una base para entender cómo se puede mapear un conjunto a otro de manera completa y eficaz.

Relevancia en otras áreas de estudio

Más allá de las matemáticas, las funciones sobreyectivas encuentran aplicabilidad en campos como la informática, la economía y la física. En la informática, por ejemplo, los conceptos de sobreyección son fundamentales para el diseño de algoritmos y la teoría de la computación, mientras que en la economía modelan relaciones entre variables de manera que se puedan comprender los fenómenos de manera íntegra y precisa.

Identificación de funciones sobreyectivas

Análisis de la imagen y codominio

Identificar una función sobreyectiva implica examinar detenidamente su imagen y codominio. La clave está en verificar que para cada elemento en el codominio exista, al menos, un elemento en el dominio que lo mapee. Este análisis no solo es fundamental para comprender la esencia de la sobreyección, sino también para aplicar correctamente estos conceptos.

Métodos para probar la sobreyección

Existen diversos métodos para demostrar la sobreyección de una función. Uno de los más directos es procurar encontrar una expresión para la inversa de la función, evidenciando así que para cada elemento en el codominio existe un correspondiente en el dominio. Otra técnica involucra el análisis del comportamiento de la función en los extremos y su continuidad, asegurando su carácter sobreyectivo.

Desafíos en el estudio de sobreyectivas

Situaciones complejas y su resolución

El estudio de las funciones sobreyectivas no está exento de desafíos, especialmente cuando se abordan funciones de naturaleza más compleja o en contextos de dimensiones superiores. La resolución de estas situaciones demanda un profundo entendimiento teórico y la habilidad de aplicar técnicas avanzadas de análisis y cálculo, superando así los obstáculos que se presenten.

Conclusión

Las funciones sobreyectivas no solo son fundamentales para las matemáticas, sino que su estudio y comprensión enriquecen nuestro acercamiento a los problemas y fenómenos del mundo real. Desde la simplicidad de una línea recta hasta la complejidad de los polinomios, las sobreyectivas nos invitan a explorar las profundidades de la matemática con curiosidad y empeño. El viaje a través de la sobreyección es, sin duda, un viaje que vale la pena emprender.

Video Relacionado sobre Funcion Sobreyectiva

FAQ Acerca de Funcion Sobreyectiva

¿Qué características tiene una función sobreyectiva?

Una función sobreyectiva se distingue principalmente por su capacidad de mapear al menos un elemento del conjunto de entrada (dominio) a cada elemento del conjunto de salida (codominio). Esto implica que cada valor que puede tomarse como salida de la función tiene asociado al menos un valor de entrada, garantizando que no existan valores "sin cubrir" en el conjunto de salida. Fundamentalmente, esto significa que el recorrido (los valores efectivamente alcanzados) es igual al codominio. Esta propiedad define completamente a la función sobreyectiva y la distingue de otros tipos de funciones, tales como las inyectivas (donde no pueden haber dos entradas con la misma salida) o las biyectivas (que son simultáneamente inyectivas y sobreyectivas).

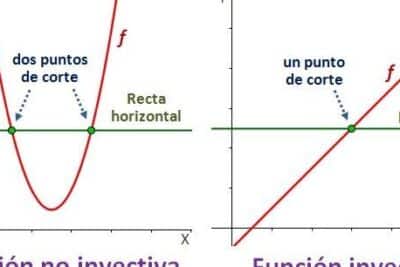
¿Cómo identificar una función sobreyectiva a través de su gráfica?

Para identificar visualmente si una función es sobreyectiva, podemos observar su representación gráfica en un plano. El criterio clave es verificar que cada valor horizontal (del codominio) se encuentre interceptado al menos una vez por la curva o línea que representa a la función. En otras palabras, si al trazar líneas horizontales estas interceptan en al menos un punto a la gráfica de la función, estamos ante una función sobreyectiva. Esta técnica visual es muy útil para obtener rápidamente una idea de la sobreyectividad de la función, aunque para una confirmación formal se requiere análisis algebraico.

¿Por qué es importante la sobreyectividad en las matemáticas?

La sobreyectividad de una función es un concepto matemático crucial porque asegura que para cada posible salida, existe al menos una entrada que la produce. Esta correspondencia completa tiene importantes aplicaciones en diversas áreas de las matemáticas y sus aplicaciones, incluidas la teoría de funciones, la estadística y la optimización. En el contexto de las ecuaciones, por ejemplo, una función sobreyectiva garantiza que cada valor en el rango tiene solución, lo que es fundamental para la resolución de ecuaciones y sistemas de ecuaciones. En la práctica, puede aplicarse para asegurar que todos los casos posibles han sido considerados en un análisis o diseño.

¿Cómo difiere una función sobreyectiva de una inyectiva?

Una función sobreyectiva y una inyectiva difieren en sus criterios de correspondencia entre los conjuntos de entrada y salida. Mientras que una función sobreyectiva requiere que cada elemento del conjunto de salida tenga al menos un preimagen en el conjunto de entrada, una función inyectiva establece que cada elemento del conjunto de entrada se mapea a elementos distintos en el conjunto de salida. Es decir, en una función inyectiva, no pueden haber dos entradas diferentes con la misma salida. Así, mientras la sobreyectividad se enfoca en cubrir completamente el conjunto de salida, la inyectividad se asegura de que no haya "choques" o duplicados en las asignaciones de entrada a salida.

¿Puede darme un ejemplo sencillo de función sobreyectiva?

Un ejemplo clásico de función sobreyectiva sería la función real f(x) = x^2 en el conjunto de los reales positivos y cero. Para cada elemento y en el conjunto de salida (y ≥ 0), podemos encontrar al menos un valor x en el conjunto de entrada (x perteneciente a los reales) tal que x^2 = y. Por ejemplo, para y = 4, tanto x = 2 como x = -2 satisfacen la ecuación x^2 = 4. Aunque la función x^2 no es sobreyectiva en todo el conjunto de los números reales (porque no puede producir números negativos como salida), es sobreyectiva en el conjunto de los reales no negativos, ilustrando cómo la naturaleza de la sobreyectividad puede depender del dominio y codominio considerados.

Si quieres conocer otros artículos parecidos a Qué define a una función sobreyectiva y ejemplos puedes visitar la categoría MATEMÁTICAS.