Qué define y caracteriza a la función logarítmica

• Las funciones logarítmicas, fundamentales en matemáticas, son el resultado inverso de las funciones exponenciales, operando bajo el dominio de los números reales positivos.
• Distinguibles por su crecimiento, que depende directamente de la base empleada, estas funciones destacan por su propiedad inyectiva, garantizando una correspondencia única entre los elementos de sus conjuntos.
• Al representarlas gráficamente, se observa una clara simetría con sus contrapartes exponenciales en relación con la bisectriz de los cuadrantes primero y tercero, reflejando su interconexión inversa.
• Este tipo de función se caracteriza por puntos clave, como (1,0) y (a,1), dependiendo de la base.
• Para la resolución de ecuaciones que las involucran, frecuentemente se transforman en equivalentes exponenciales, lo cual simplifica su análisis y solución, demostrando su versatilidad y aplicabilidad en diversos contextos matemáticos.

Las matemáticas son un mundo fascinante, lleno de conceptos intrigantes y aplicaciones prácticas. Dentro de este universo, las funciones logarítmicas ocupan un lugar especial, siendo herramientas poderosas tanto en la teoría como en la práctica. Este artículo desentrañará los misterios que definen y caracterizan a las funciones logarítmicas, abriendo puertas al entendimiento y la aplicación de este concepto matemático.

Al adentrarnos en este viaje, exploraremos desde la definición fundamental hasta las propiedades únicas que las hacen destacar, su relación inversa con las funciones exponenciales, y cómo estas funciones se aplican en la solución de ecuaciones y se representan gráficamente. Prepárate para sumergirte en el fascinante mundo de las funciones logarítmicas.

Definición de función logarítmica

En palabras simples, una función logarítmica es aquella en la que el logaritmo de una variable es directamente proporcional a otra variable. Matemáticamente, se expresa como (y = log_b(x)), donde (y) es el logaritmo de (x) con base (b). Esta definición plantea la base para comprender cómo estas funciones modelan relaciones inversas y proporcionales en el mundo real y matemático.

Importancia de la base logarítmica

La base de un logaritmo es fundamental porque determina la curvatura de su gráfico y el ritmo de crecimiento o decrecimiento de la función. Las bases más comunes son el número de Euler (e) (base natural), y 10 (base decimal), cada una con sus propias aplicaciones específicas en ciencias, ingeniería, y matemáticas financieras.

Dominio y rango

El dominio de una función logarítmica comprende todos los números reales positivos, excluyendo el cero, ya que el logaritmo de cero es indefinido. El rango, por otro lado, abarca todos los números reales. Esto implica que una función logarítmica puede tomar cualquier valor de (y) para un (x) positivo dado.

La inversión de funciones exponenciales

Relación con la exponencial

Las funciones logarítmicas y exponenciales son inversas una de otra. Esto significa que si (y = b^x), entonces (x = log_b(y)). Esta relación inversa es la clave para comprender cómo operan en conjunto para modelar situaciones de crecimiento exponencial y decaimiento.

Simetría respecto a la bisectriz

Gráficamente, las funciones logarítmicas y exponenciales son simétricas entre sí respecto a la bisectriz de los cuadrantes primero y tercero. Este fenómeno refleja su naturaleza inversa y proporciona una herramienta visual para entender cómo se transforma una función en la otra a través de la reflexión.

Propiedades fundamentales

Inyectividad de las logarítmicas

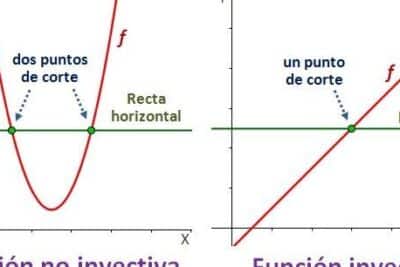
Una propiedad clave de las funciones logarítmicas es su inyectividad. Esto significa que para cada valor en el rango, existe un único valor en el dominio que corresponde, haciendo a las funciones logarítmicas herramientas perfectas para ecuaciones donde se requiere precisión y unicidad en las soluciones.

Crecimiento según la base

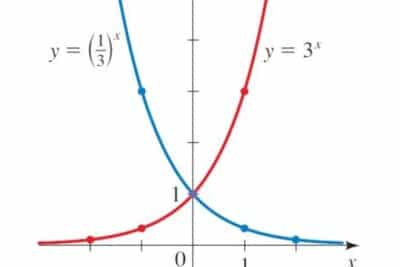
El comportamiento de crecimiento de las funciones logarítmicas varía según su base; si la base es mayor que 1, la función crece, mientras que si la base es menor que 1 (pero aún positiva), la función decrece. Este comportamiento es crucial para modelar fenómenos que escalan en orden de magnitud a diferentes ritmos.

Aplicación en ecuaciones

Estrategias de resolución

Resolver ecuaciones logarítmicas a menudo implica primero identificar la base y luego usar propiedades logarítmicas para simplificar o transformar la ecuación en una forma más manejable. Estrategias como el uso de logaritmos de igual base pueden simplificar la resolución de ecuaciones complejas.

Transformación a exponenciales

Una técnica poderosa en la resolución de ecuaciones logarítmicas es transformarlas en sus equivalentes exponenciales. Esto aprovecha la relación inversa entre logaritmos y exponenciales para encontrar soluciones que a veces son menos evidentes en su forma logarítmica.

Representación gráfica

Puntos clave en el gráfico

En la gráfica de una función logarítmica, puntos como ( (1,0) ) y ( (b,1) ) son cruciales porque marcan la intersección con los ejes y el punto donde la función evalúa a 1, respectivamente. Estos puntos clave ayudan a trazar la curva característica de la función logarítmica.

Interpretación visual

La representación gráfica de funciones logarítmicas ofrece una interpretación visual de cómo el cambio en la base afecta la forma de la curva. Observar estas gráficas permite entender la velocidad a la que crece o decrece la función, ofreciendo insights valiosos para la modelación de fenómenos.

Concluir este viaje por el mundo de las funciones logarítmicas nos deja con un entendimiento profundo de su naturaleza, propiedades, y aplicaciones. Hemos visto cómo estas funciones no solo modelan la realidad de formas intrigantes sino que también son fundamentales en el campo de las matemáticas para resolver ecuaciones y comprender el comportamiento exponencial. Al dominar los principios y aplicaciones de las funciones logarítmicas, se abre un abanico de posibilidades para explorar, entender y manipular el mundo a través de las matemáticas.

Video Relacionado sobre Funcion Logaritmica

FAQ Acerca de Funcion Logaritmica

¿Qué define a la función logarítmica?

Una función logarítmica se caracteriza por ser el proceso inverso a la función exponencial, representando operaciones donde un número específico, conocido como la base, debe ser elevado a una potencia para igualar otro número. Este tipo de función se emplea ampliamente para describir fenómenos cuyo crecimiento o decrecimiento es proporcional a su estado actual, lo que la hace fundamental en diversas áreas del conocimiento incluyendo la matemática, la física y la biología.
La función logarítmica tiene propiedades únicas: es definida solo para números reales positivos, siendo su dominio exclusivo de estos, y puede ser transformada a una línea recta bajo ciertas condiciones, lo cual simplifica su estudio y representación gráfica. Además, desempeña un papel crucial en la solución de ecuaciones exponenciales, ya que, al ser la inversa de la función exponencial, permite reescribir y resolver estas ecuaciones de manera más accesible.

¿Cómo se resuelven las ecuaciones logarítmicas?

Resolver ecuaciones logarítmicas comienza por entender la relación entre los logaritmos y las exponenciales, ya que convertir logaritmos en sus formas exponenciales equivalentes es uno de los pasos fundamentales. El objetivo es reorganizar la ecuación hasta que el logaritmo se encuentre aisladamente en un lado de la igualdad, facilitando su conversión a una ecuación exponencial. Este proceso a menudo requiere el uso de propiedades logarítmicas básicas, como las reglas de los logaritmos para sumar, restar, y la potencia de logaritmos. Una vez convertida, la ecuación se resuelve en términos de su variable, posibilitando hallar el valor específico que satisface la igualdad original.
El manejo fluido de las propiedades algebraicas y logarítmicas es crucial para encarar estas ecuaciones. Además, en contextos más avanzados, se pueden emplear técnicas como el cambio de variable para simplificar aún más la solución, lo cual es especialmente útil en ecuaciones logarítmicas complejas o aquellas que involucran múltiples términos logarítmicos.

¿Qué indica el punto (1,0) en su gráfica?

El punto (1,0) es un punto característico en la gráfica de cualquier función logarítmica debido a una propiedad fundamental de los logaritmos: el logaritmo de 1 en cualquier base es 0. Este punto es un indicativo de que, sin importar la base del logaritmo (siempre y cuando sea positiva y diferente de 1), el resultado de aplicar la función logarítmica al número 1 siempre será 0. Este comportamiento ofrece una referencia visual clave para el trazado y análisis de la gráfica logarítmica, sirviendo como punto de partida para comprender su comportamiento respecto a la base escogida. Al graficar, este punto ayuda a establecer una simetría con respecto a la función exponencial y marca uno de los ejes de referencia cruciales en el estudio de estas funciones.

¿Qué rol juega la base en las funciones?

La base de una función logarítmica es el número positivo diferente de 1 sobre el cual se construye el logaritmo. Esta base determina la rapidez con la que crece o decrece la función y su dirección (creciente si la base es mayor que 1, decreciente si es entre 0 y 1). La elección de la base está estrechamente relacionada con el contexto de aplicación de la función logarítmica; por ejemplo, el logaritmo natural (base e, aproximadamente 2.71828) es ampliamente utilizado en matemáticas y ciencias debido a sus propiedades inherentes que simplifican el cálculo diferencial e integral. Cambiar la base altera la pendiente de la gráfica logarítmica, pero no sus propiedades fundamentales, como su dominio y su naturaleza inyectiva. Cada base aporta una lente distinta a través de la cual se puede examinar el crecimiento exponencial y su inverso, aportando una herramienta versátil para la modelación de fenómenos naturales y matemáticos.

¿Por qué son importantes en ciencias e ingeniería?

Las funciones logarítmicas son herramientas indispensables en ciencias e ingeniería debido a su capacidad para modelar y resolver problemas relacionados con el crecimiento exponencial y los procesos de descomposición, áreas donde fenómenos como la desintegración radiactiva, el crecimiento de poblaciones, y la atenuación de señales se describen naturalmente mediante estas funciones. En ingeniería, su utilidad se extiende al diseño y análisis de circuitos, la acústica, y la gestión de la información, como en la compresión de datos y la medida de la información (entropía). Las funciones logarítmicas facilitan el manejo de grandes cantidades y escalas ampliamente variables, transformándolas en magnitudes manejables y comparables. Su aplicación en el análisis de series temporales, la probabilidad, y estadísticas subraya aún más su relevancia, demostrando su papel fundamental en la simplificación y resolución de problemas complejos en múltiples disciplinas.

Si quieres conocer otros artículos parecidos a Qué define y caracteriza a la función logarítmica puedes visitar la categoría MATEMÁTICAS.