Qué son los ángulos adyacentes Características y ejemplos

• Los ángulos adyacentes guardan secretos matemáticos que nos revelan mucho más sobre la geometría de lo que podríamos imaginar a primera vista.
• Al considerar esta intrigante figura geométrica, forjada por la reunión de dos semirrectas que comparten no solo un origen sino un propósito, nos adentramos en un mundo donde la suma de sus espacios abiertos es siempre de 180°.
• Esta característica es fundamental, ya que nos permite entender mejor cómo se relacionan y complementan dentro de un plano.

  Sin embargo, al traspasar la superficie de lo que un ángulo adyacente representa, nos encontramos con discrepancias y matices en su definición, lo que agrega un nivel de profundidad y debate académico sobre su verdadera esencia.

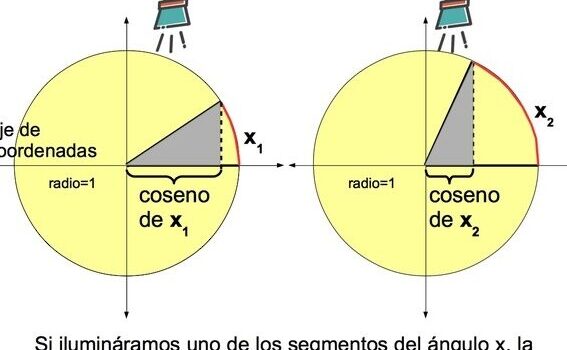
• Además, estas criaturas geométricas nos susurran verdades trigonométricas a través de sus cosenos y senos, funciones que, a pesar de la simplicidad que presentan en un triángulo rectángulo, son capaces de caracterizar cualquier ángulo mediante la relación exacta entre sus lados.

  El coseno, describiendo la danza entre el cateto adyacente y la hipotenusa, contrasta con el seno, que narra la historia de unión entre el cateto opuesto y la hipotenusa.

• A pesar de que sus caminos son distintos, comparten la belleza de la proporción y la medida, iluminando el camino hacia una comprensión más profunda de la geometría.

  Los ejercicios resueltos nos llevan de la mano a través de exquisitos ejemplos prácticos, permitiéndonos vivenciar la aplicación real de estos conceptos.

• Cada problema de ángulos adyacentes se convierte en una historia a resolver, donde los números y las proporciones son los protagonistas, desentrañando así los misterios que estas uniones angulares guardan pacientemente.

Los ángulos adyacentes son una parte fundamental de la geometría y la trigonometría. Exploraremos en detalle qué son los ángulos adyacentes, sus características principales y cómo se utilizan en diferentes contextos. Además, discutiremos las propiedades de los ángulos adyacentes, su importancia en la geometría y la trigonometría, y cómo se pueden identificar y resolver problemas que involucran este tipo de ángulos. También aprenderemos cómo se diferencian de otros tipos de ángulos, como los ángulos complementarios y suplementarios. ¡Vamos a sumergirnos en el fascinante mundo de los ángulos adyacentes!

Definición de ángulos adyacentes

Los ángulos adyacentes son aquellos que comparten un lado y un vértice común. En otras palabras, los lados de dos ángulos adyacentes se superponen parcialmente y comparten un punto en común, que es el vértice del ángulo. Esta relación entre los ángulos adyacentes crea una forma continua o continua.

Características principales

Una de las características principales de los ángulos adyacentes es que su suma siempre es igual a 180 grados. Esto significa que cuando se colocan dos ángulos adyacentes lado a lado, la medida total de los dos ángulos siempre será igual a un ángulo recto (90 grados). Esta propiedad es útil al resolver problemas geométricos y trigonométricos que implican ángulos adyacentes.

Además, es importante tener en cuenta que los ángulos adyacentes pueden estar en diferentes posiciones en relación con otros ángulos. Pueden ser adyacentes internamente o externamente a otros ángulos. Los ángulos adyacentes internos son aquellos que se encuentran dentro de otro ángulo más grande, mientras que los ángulos adyacentes externos son aquellos que se encuentran fuera de otro ángulo más grande.

Ejemplos claros

Para entender mejor qué son los ángulos adyacentes, veamos algunos ejemplos claros:

- En un triángulo, los dos ángulos adyacentes a un lado compartido son ángulos adyacentes externos.
- Si tenemos un ángulo de 30 grados, los ángulos adyacentes a este pueden ser uno de 60 grados y otro de 90 grados.
- En un cuadrado, los cuatro ángulos adyacentes son de 90 grados cada uno.

Estos ejemplos ilustran cómo los ángulos adyacentes aparecen en diferentes formas geométricas y cómo su suma siempre es igual a 180 grados.

Propiedades de los ángulos adyacentes

Además de su suma siempre ser igual a 180 grados, los ángulos adyacentes tienen otras propiedades interesantes que pueden ayudarnos a resolver problemas geométricos y trigonométricos.

Suma de 180 grados

Como mencionamos anteriormente, la propiedad más destacada de los ángulos adyacentes es que su suma siempre es igual a 180 grados. Esto se debe a que los ángulos adyacentes comparten un lado y un vértice común, lo que significa que la medida total de los dos ángulos resultará en un ángulo recto.

Por ejemplo, si tenemos un ángulo de 45 grados y otro ángulo adyacente a él, la suma de los dos ángulos será de 45 grados + 135 grados = 180 grados.

Esta propiedad es esencial al trabajar con ángulos adyacentes, ya que nos permite realizar cálculos y resolver problemas de manera más eficiente.

Igualdad de senos

Otra propiedad interesante de los ángulos adyacentes es que sus senos son iguales. El seno es una función trigonométrica que relaciona la longitud del cateto opuesto a un ángulo agudo en un triángulo rectángulo con la longitud de la hipotenusa. En este caso, los ángulos adyacentes no necesariamente tienen que ser parte de un triángulo rectángulo, pero la propiedad aún se mantiene.

Por ejemplo, si tenemos un ángulo de 30 grados y otro ángulo adyacente a él, ambos ángulos tendrán el mismo seno. Esto significa que para ambos ángulos, la razón entre la longitud del lado opuesto a ese ángulo y la longitud de la hipotenusa será la misma.

Cosenos con signos opuestos

Además de tener senos iguales, los ángulos adyacentes también tienen cosenos con signos opuestos. El coseno es otra función trigonométrica que relaciona la longitud del cateto adyacente a un ángulo agudo en un triángulo rectángulo con la longitud de la hipotenusa. Al igual que con la propiedad anterior, los ángulos adyacentes no necesariamente tienen que ser parte de un triángulo rectángulo, pero la propiedad aún se mantiene.

Por ejemplo, si tenemos un ángulo de 45 grados y otro ángulo adyacente a él, ambos ángulos tendrán el mismo valor absoluto para el coseno, pero con signos opuestos. Esto significa que para ambos ángulos, la razón entre la longitud del lado adyacente a ese ángulo y la longitud de la hipotenusa será la misma, pero con signos opuestos.

Estas propiedades son fundamentales en la geometría y la trigonometría, ya que nos permiten relacionar los ángulos adyacentes con otras medidas y propiedades geométricas.

Importancia en geometría

Los ángulos adyacentes desempeñan un papel importante en la geometría, ya que nos ayudan a comprender y analizar diferentes figuras y formas geométricas.

Uso en figuras geométricas

En diferentes figuras geométricas, como triángulos, cuadrados y polígonos en general, los ángulos adyacentes son una propiedad clave que debemos tener en cuenta al calcular áreas, perímetros y propiedades de las figuras.

Por ejemplo, al calcular el área de un triángulo utilizando la fórmula del área base-altura, los ángulos adyacentes pueden ayudarnos a determinar la longitud de la altura correspondiente a la base elegida.

Además, al calcular el perímetro de un polígono, debemos tener en cuenta los ángulos adyacentes para determinar los lados que los conectan y su longitud total.

Los ángulos adyacentes son fundamentales en la geometría para analizar y calcular propiedades de diferentes figuras geométricas.

Relevancia en trigonometría

En trigonometría, los ángulos adyacentes son de vital importancia, ya que nos permiten aplicar las funciones trigonométricas como el seno, el coseno y la tangente.

Al calcular las razones trigonométricas de un ángulo, como el seno y el coseno, podemos utilizar los ángulos adyacentes para determinar las longitudes de los lados del triángulo rectángulo correspondiente.

Por ejemplo, si tenemos un ángulo de 30 grados y queremos calcular el seno de ese ángulo, podemos utilizar un ángulo adyacente para determinar la longitud del cateto opuesto y la longitud de la hipotenusa en el triángulo rectángulo correspondiente.

En definitiva, los ángulos adyacentes son esenciales en la trigonometría para relacionar las medidas de los ángulos agudos con las propiedades de los triángulos rectángulos.

Identificación en ejercicios

Identificar los ángulos adyacentes en ejercicios y problemas puede ser crucial para resolverlos de manera correcta. Aquí te mostraremos algunas técnicas de medición y resolución de problemas que te ayudarán a identificar y trabajar con ángulos adyacentes.

Técnicas de medición

Una forma común de identificar ángulos adyacentes es utilizando un transportador. Un transportador es una herramienta utilizada para medir y trazar ángulos. Al colocar el vértice del ángulo en el punto central del transportador y alinear uno de los lados del ángulo con una de las líneas del transportador, podemos determinar la medida del ángulo en grados.

Al medir un ángulo, es importante comparar los lados del ángulo para determinar si son adyacentes o no. Si los lados se superponen parcialmente y comparten un punto en común, entonces los ángulos son adyacentes.

Otra técnica de medición es utilizar la propiedad de la suma de los ángulos adyacentes. Si conocemos la medida de uno de los ángulos adyacentes y la suma total de los ángulos es igual a 180 grados, entonces podemos determinar la medida del otro ángulo adyacente.

Resolución de problemas

Al resolver problemas geométricos o trigonométricos que involucran ángulos adyacentes, es importante tener en cuenta las propiedades que discutimos anteriormente.

Por ejemplo, si se te presenta un problema en el que tienes que determinar la medida de un ángulo adyacente a otro ángulo dado, puedes utilizar la propiedad de la suma de los ángulos adyacentes. Si conoces la medida total de los ángulos y la medida de uno de los ángulos adyacentes, puedes restar la medida conocida del ángulo adyacente de la suma total para determinar la medida del otro ángulo adyacente.

También puedes utilizar las propiedades trigonométricas de los ángulos adyacentes, como la igualdad de senos y los cosenos con signos opuestos, para resolver problemas trigonométricos que involucran ángulos adyacentes.

Al identificar ángulos adyacentes en ejercicios y problemas, es crucial utilizar técnicas de medición y aplicar las propiedades y fórmulas pertinentes para resolverlos de manera precisa y eficiente.

Diferencias con otros tipos de ángulos

Es importante comprender las diferencias entre los ángulos adyacentes y otros tipos de ángulos para evitar confusiones y errores al trabajar con ellos.

Comparación con ángulos complementarios

Los ángulos complementarios son aquellos que suman 90 grados; es decir, su suma es un ángulo recto. A diferencia de los ángulos adyacentes, los ángulos complementarios no comparten un lado y un vértice común. En cambio, están ubicados uno al lado del otro en una forma opuesta o en ángulos opuestos. Esto significa que los ángulos complementarios no tienen un punto en común entre sus lados.

Por ejemplo, si tenemos un ángulo de 30 grados, su ángulo complementario será de 60 grados. Estos ángulos no son adyacentes, ya que no comparten un lado y vértice común.

Comparación con ángulos suplementarios

Los ángulos suplementarios son aquellos que suman 180 grados; es decir, su suma es un ángulo llano. A diferencia de los ángulos adyacentes, los ángulos suplementarios no comparten un lado y un vértice común. Al igual que los ángulos complementarios, los ángulos suplementarios están ubicados uno al lado del otro en una forma opuesta o en ángulos opuestos.

Por ejemplo, si tenemos un ángulo de 60 grados, su ángulo suplementario será de 120 grados. Estos ángulos no son adyacentes, ya que no comparten un lado y vértice común.

Los ángulos adyacentes son aquellos que comparten un lado y un vértice común, y su suma siempre es igual a 180 grados. Son utilizados en geometría y trigonometría para calcular propiedades y resolver problemas relacionados con figuras geométricas y triángulos rectángulos. Al identificar ángulos adyacentes en ejercicios y problemas, es importante utilizar técnicas de medición y aplicar las propiedades y fórmulas pertinentes. Además, es fundamental entender las diferencias entre los ángulos adyacentes y otros tipos de ángulos, como los ángulos complementarios y suplementarios.

Video sobre Angulos Adyacentes

Preguntas Frecuentes sobre Angulos Adyacentes

¿Cómo se identifican ángulos adyacentes?

Para identificar ángulos adyacentes, es crucial observar que deben cumplir con dos condiciones esenciales: en primer lugar, deben compartir un vértice común que actúe como el punto de unión de las semirrectas que conforman los ángulos. En segundo lugar, deben compartir un lado, es decir, una de estas semirrectas debe formar parte de ambos ángulos. Esta configuración hace que los ángulos adyacentes se desplieguen en una línea recta, por tanto, deben sumar 180°. Esta característica es fundamental para su aplicación en problemas geométricos y trigonométricos, facilitando el estudio de diversas figuras y patrones en matemáticas.

¿Qué importancia tienen los senos y cosenos?

Los senos y cosenos son fundamentales en trigonometría, especialmente al trabajar con ángulos adyacentes. El seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto al ángulo y la hipotenusa. Por otro lado, el coseno se determina por la relación entre el cateto adyacente al ángulo y la hipotenusa. En el contexto de ángulos adyacentes, la relación de sus senos es igual, lo que significa que la proporción de su cateto opuesto respecto a la hipotenusa es la misma, ofreciendo una mirada interesante a su simetría y balance. En cuanto a los cosenos, aunque sus valores absolutos son iguales, sus signos son opuestos, reflejando cómo se distribuyen en el plano cartesiano. Estas relaciones son clave no solo para resolver ejercicios de trigonometría, sino también para entender las propiedades de las figuras geométricas y sus simetrías.

¿Todos los ángulos adyacentes suman 180°?

Sí, una característica definitoria de los ángulos adyacentes es que, al compartir un lado y estar ubicados en una línea recta, su suma siempre debe ser igual a 180°. Esta propiedad se conoce como suplementariedad y es crucial tanto para la resolución de problemas de geometría como para la comprensión de la estructura de figuras planas. Si dos ángulos no cumplen con esta condición, entonces no se consideran adyacentes. Esta regla proporciona una base fundamental para el estudio y análisis de patrones geométricos, figuras y demostraciones en el amplio campo de la matemáticas.

¿Cómo afecta la discrepancia de definiciones?

Aunque la definición básica de ángulos adyacentes es generalmente aceptada, las discrepancias en detalles específicos pueden surgir en diferentes textos o contextos académicos. Estas diferencias suelen centrarse en la interpretación de propiedades o en la aplicación de estos ángulos en contextos más complejos. Sin embargo, es importante destacar que el núcleo fundamental —compartir un vértice y un lado, y sumar 180°— se mantiene constante. Las variaciones en la definición no afectan significativamente la comprensión básica de estos ángulos, pero sí pueden influir en cómo se abordarán o se resolverán problemas específicos en niveles más avanzados de estudio.

¿Por qué es relevante su coseno y seno?

La relevancia de los cosenos y senos en ángulos adyacentes reside en cómo estos valores trigonométricos facilitan la descripción y solución de problemas geométricos y físicos. En el caso de los ángulos adyacentes, el hecho de que sus senos sean iguales y sus cosenos tengan el mismo valor absoluto pero con signos opuestos, permite aplicaciones en ingeniería, arquitectura, diseño y ciencias físicas, donde la precisión y la comprensión de las relaciones espaciales son fundamentales. Estos valores son claves para transformar y manipular figuras geométricas, optimizar diseños y resolver problemas reales que involucran el movimiento y las fuerzas en el espacio.

Si quieres conocer otros artículos parecidos a Qué son los ángulos adyacentes Características y ejemplos puedes visitar la categoría CIENCIAS.