Múltiplo: Definición, Propiedades y Ejemplos Claros

• Explorar el universo de los múltiplos es sumergirse en un concepto matemático y gramatical fundamental.
• Un múltiplo resulta de multiplicar un número por otro, como cuando 12 es múltiplo de 3 (3x4=12).
• Identificarlos es sencillo mediante la división: si el resto es cero, estamos ante un múltiplo.
• Los múltiplos tienen propiedades intrigantes, como la infinitud o la relación con los divisores.
• Además, convergen en contextos diarios y científicos, aportando soluciones prácticas, desde la aritmética hasta la conversión de unidades de medida.
• Los submúltiplos contrastan, permitiendo entender otra faceta de la estructura numérica.
• Finalmente, en la gramática, los múltiplos transforman la manera de expresar cantidades, aportando precisión y claridad al lenguaje.

Explorar el mundo de los múltiplos puede ser tan intrigante como atravesar un laberinto de números, donde cada giro desvela nuevos enigmas y soluciones. Este viaje matemático revela la fascinante armonía entre los números y su aplicación práctica a nuestro alrededor.

Desenredaremos la complejidad de los múltiplos, sus propiedades y ejemplos claros que iluminarán este concepto fundamental en matemáticas. Prepárese para un profundo buceo en el universo de los múltiplos.

Qué es un múltiplo

En las matemáticas, entender qué es un múltiplo es fundamental. Un número entero es considerado múltiplo de otro si el primero puede ser dividido exactamente por el segundo sin dejar resto. Dicho de otra forma, si multiplicamos un número entero por cualquier otro número entero, el resultado es un múltiplo del primer número.

Formas de identificar múltiplos

Hay varias formas de identificar si un número es múltiplo de otro. El método más sencillo es realizar una división; si el residuo es cero, entonces, definitivamente estamos frente a un múltiplo. Otra forma es el reconocimiento de patrones, especialmente útil con múltiplos de números como 5, 10 o 2, donde las cifras finales siguen patrones determinados.

Propiedades fundamentales de los múltiplos

Los múltiplos están regidos por ciertas propiedades destacables muy interesantes. Una de ellas es que el número cero es múltiplo de cualquier número. Por otro lado, cualquier número es múltiplo de sí mismo y de uno. Estas propiedades dotan a los múltiplos de una versatilidad única en el ámbito de las matemáticas.

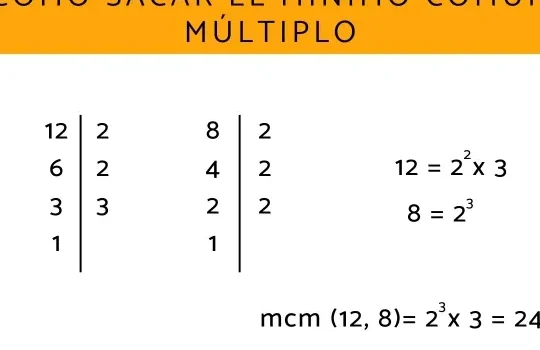
Múltiplos comunes y mínimos

Los múltiplos comunes son números que son múltiplos de dos o más números al mismo tiempo. Dentro de este conjunto, el mínimo múltiplo común (MMC) es especialmente significativo, ya que es el menor número que es múltiplo de todos ellos. Esta propiedad es esencial en la resolución de problemas de fracciones y problemas matemáticos más complejos.

Relación con divisores

La relación entre múltiplos y divisores es estrecha y fundamental. Mientras que un múltiplo es un número que contiene a otro cierto número de veces de manera exacta, un divisor es un número que se puede “extraer” de otro número también de manera exacta. Cada uno ofrece una perspectiva diferente sobre la estructura y las relaciones entre números.

Ejemplos claros de múltiplos

Múltiplos de números sencillos

Para ilustrar, consideremos el número 5. Los múltiplos de 5 son fácilmente identificables: 10, 15, 20, 25, y así sucesivamente. Estos múltiplos siguen un patrón predecible, aumentando de cinco en cinco.

Múltiplos en situaciones cotidianas

Los múltiplos también se encuentran en situaciones cotidianas. Por ejemplo, al comprar huevos por docenas, estamos manejando el concepto de múltiplos de 12. A través de esta sencilla acción, los múltiplos se integran a nuestra vida diaria, demostrando su relevancia y aplicabilidad.

Aplicaciones prácticas de múltiplos

En la ciencia y tecnología

En la ciencia y la tecnología, los múltiplos desempeñan un rol crucial. Por ejemplo, en la informática, las unidades de almacenamiento (bytes) siguen una secuencia basada en múltiplos de 8. Esta relación subyacente impulsa el desarrollo y la estandarización de tecnologías.

En la vida diaria

Más allá de las aulas escolares, los múltiplos juegan un papel vital en nuestra vida cotidiana, desde la organización de eventos, que pueden requerir la comprensión de múltiplos para la distribución de invitaciones, hasta la cocina, donde las recetas a menudo implican medir ingredientes en múltiplos de una medida básica.

Identificación de múltiplos en matemáticas

Cálculo de múltiplos

Identificar y calcular múltiplos puede parecer una tarea ardua, pero con práctica y comprensión de las propiedades básicas de los múltiplos, se convierte en una actividad matemática manejable y hasta entretenida. Al dominar técnicas simples como la división y el reconocimiento de patrones, cualquier persona puede convertirse en un maestro en la identificación de múltiplos.

Submúltiplos: Concepto y ejemplos

Diferencias entre múltiplos y submúltiplos

Los submúltiplos, aunque menos mencionados, son tan fundamentales como los múltiplos. Un submúltiplo es, esencialmente, un divisor. La principal diferencia radica en la perspectiva: mientras que consideramos a un número como múltiplo cuando es resultado de multiplicar otra cifra, lo consideramos submúltiplo cuando es la cifra inicial en la multiplicación. Este sutil giro conceptual amplía nuestra comprensión de las relaciones numéricas.

Conclusión

Los múltiplos son, sin duda alguna, una parte integral de las matemáticas y de la vida cotidiana. A través de este extenso viaje, hemos explorado su definición, propiedades, aplicaciones prácticas, y diferencia con los submúltiplos. La próxima vez que te encuentres contando, dividiendo o incluso comprando en múltiplos, recuerda la magnitud y la universalidad de estos conceptos numéricos. Los múltiplos no solo facilitan la resolución de problemas matemáticos, sino que también enriquecen nuestra comprensión del mundo.

Video Relacionado sobre Multiplo

FAQ Acerca de Multiplo

¿Qué es un múltiplo exactamente?

Un múltiplo se identifica en el ámbito de las matemáticas como un número que resulta de multiplicar un número entero, llamado base, por otro número natural. A diferencia de una operación matemática común, el concepto de múltiplo abarca una relación específica entre dos números: si al multiplicar el número natural (factor) por el base se obtiene como resultado dicho múltiplo, entonces se establece que hay una relación de múltiploidar exacta. Es importante entender que todo número es múltiplo de sí mismo y de uno, por lo que la idea de múltiplo se extiende a lo infinito para cada número, creando un conjunto ilimitado de posibilidades.

¿Cómo determinar si un número es múltiplo de otro?

Para establecer si un número es múltiplo de otro, se aplica una simple operación de división. Si al dividir el número en cuestión (que se propone como múltiplo) entre el otro número (considerado la base), el resultado de esta división es un número entero sin residuo (resto cero), entonces se confirma que el primer número es efectivamente múltiplo del segundo. Esta técnica no solo valida la relación de múltiploidar, sino que también permite entender las relaciones numéricas de manera más profunda, demostrando cómo interactúan los números entre sí en el marco de la aritmética.

¿Todos los números tienen múltiplos?

Sí, cada número, sin importar cuán grande sea, posee un set infinito de múltiplos. Esta característica inherente a los números se debe a la naturaleza misma de la multiplicación. Desde el momento en que un número puede ser multiplicado por cualquier número natural, incluido él mismo y uno, se desprende que la lista de múltiplos es interminable. Esto subraya un principio básico de los números: cada uno es una pieza fundamental en el vasto entramado de las operaciones matemáticas, conectados entre sí a través de sus múltiplos.

¿Qué propiedades tienen los múltiplos?

Los múltiplos comparten varias propiedades distintivas, entre las que destaca la relación fundamental que guardan con los números uno y el propio número base, siendo múltiplos de ambos. Además, los múltiplos de un número tienen en común ciertos divisores, estableciendo conexiones entre diversos conjuntos de números. Otra propiedad importante es su comportamiento ante las operaciones básicas: la suma o resta de dos múltiplos del mismo número resulta en otro múltiplo del mismo número, evidenciando la cohesión y consistencia interna de estos conjuntos numéricos. Estas propiedades no solo son útiles para la resolución de problemas aritméticos, sino que también ofrecen una ventana al entendimiento de las estructuras matemáticas más complejas.

¿Cómo se aplican los submúltiplos en la vida real?

Los submúltiplos tienen una relevancia práctica particularmente en el ámbito de la conversión de unidades de medida. Este concepto permite entender cómo una unidad mayor puede ser expresada como una cantidad exacta de unidades menores, facilitando operaciones como el cambio de metros a centímetros o de kilogramos a gramos. En la cotidianidad, esta comprensión ayuda tanto en actividades simples, como cocinar o medir distancias, como en aplicaciones más complejas en ciencias, ingeniería y tecnología. La habilidad para manipular y convertir unidades a través de los submúltiplos es fundamental para navegar y comprender el mundo físico y sus diversas escalas.

¿Qué relevancia tiene el concepto de múltiplo en la gramática?

En el terreno gramatical, los múltiplos se manifiestan a través de sustantivos y adjetivos numerales que expresan la idea de multiplicidad, tales como doble, triple o cuádruple. Esta notación es esencial para la comunicación precisa de cantidades específicas, especialmente en contextos donde la relación proporcional entre elementos necesita ser claramente establecida. En literatura, periodismo y redacción técnica, el uso adecuado de estos términos numerales multiplica la claridad y precisión del mensaje, permitiendo al receptor una comprensión inmediata de las relaciones cuantitativas discutidas.

Si quieres conocer otros artículos parecidos a Múltiplo: Definición, Propiedades y Ejemplos Claros puedes visitar la categoría MATEMÁTICAS.