Cosecante: Definición, Función y Concepto en Matemáticas

• Dentro del vasto universo de la trigonometría, cada función tiene su protagonismo y utilidad, siendo la cosecante una de las estrellas a menudo eclipsadas por sus contrapartes más populares.
• Originada en el corazón de los triángulos rectángulos, este concepto brilla al definirse como la relación inversa del seno, es decir, nace de dividir la longitud de la hipotenusa por el cateto opuesto.
• Imaginemos, por un momento, un triángulo con una hipotenusa que mide 10 cm y un cateto opuesto de 4 cm; en este universo bidimensional, la cosecante asciende a 2,5, un número que no solo existe en teoría sino que se demuestra prácticamente al dividir 1 entre el valor del seno del ángulo en cuestión.

  Pero, ¿dónde más podemos encontrar a esta función trigonométrica aparte de los libros de texto y los exámenes de matemáticas?

• Su aplicación trasciende la esfera académica, encontrando propósito en el reino de la programación informática y la creación de gráficos tridimensionales.
• Aquí, la cosecante, junto a sus parientes la secante y la cotangente, se convierten en herramientas cruciales para solucionar problemas geométricos y ajustar precisamente la posición de los puntos durante las transformaciones espaciales.

  Entender la función cosecante es subir un peldaño más en la comprensión de cómo las matemáticas modelan el mundo físico y digital a nuestro alrededor.

• Nos ofrece una perspectiva diferente para calcular longitudes desconocidas en triángulos rectángulos, siempre que tengamos datos sobre uno de sus ángulos y lados.
• Cosecante no es solo una función más en la trigonometría; es una ventana a dimensiones geométricas y aplicaciones prácticas que demuestra cómo los números dan forma a nuestra realidad.

En el vasto universo de la matemáticas, existen funciones y conceptos que son esenciales para comprender y solucionar problemas de diferentes áreas. Una de estas funciones es la cosecante, componente crucial en el estudio de la trigonometría. Este artículo profundiza en esta función, trazando un camino desde su definición hasta sus aplicaciones, sin dejar de lado sus peculiaridades y comparativas.

Damos un paso adelante, navegando por las aguas de la comprensión matemática para desentrañar el significado y la importancia de la función cosecante, permitiendo a cualquier lector, sea neófito o veterano en trigonometría, obtener una visión completa sobre este tema.

Definición de cosecante

La cosecante es una de las seis funciones trigonométricas fundamentales, pero a menudo es menos comprendida o mencionada que sus más famosas contrapartes como el seno y el coseno. En su esencia, define una relación específica dentro de un triángulo rectángulo.

Relación con el seno

Para entender profundamente la cosecante, es indispensable abordar su relación intrínseca con el seno. Matemáticamente, la cosecante (csc) de un ángulo es el recíproco del seno de ese mismo ángulo. En términos del cálculo trigonométrico, si se tiene un seno de valor 'x', la cosecante será 1/x.

Función cosecante en trigonometría

La función cosecante se representa en la trigonometría como csc(θ), donde θ es un ángulo. Desempeña un papel crucial en varias operaciones y fórmulas trigonométricas, facilitando el cálculo de distancias y ángulos en contextos variados.

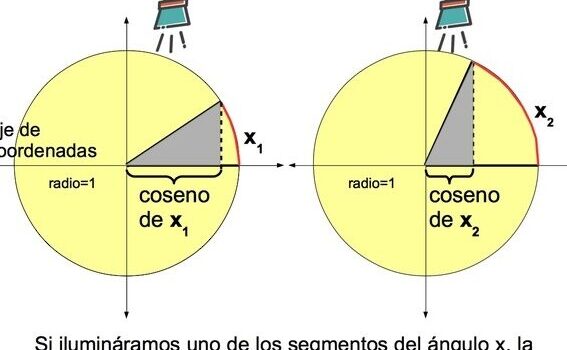
Representación gráfica

La gráfica de la función cosecante es peculiar y distinta a la mayoría de las funciones. Se compone de una serie de arcos infinitamente largos, donde cada punto representa el recíproco del seno de un ángulo específico. Esta forma permite visualizar sus propiedades de periodicidad y amplitud de manera intuitiva.

Importancia de la cosecante

La función cosecante, a pesar de ser menos mencionada que otras funciones trigonométricas, tiene una relevancia significativa en diversos campos y aplicaciones. Su comprensión e implementación son fundamentales para la resolución de problemas en ingeniería, física y otras ciencias.

Aplicaciones prácticas

Una de las principales aplicaciones de la cosecante se encuentra en la resolución de problemas que implican modelado de fenómenos físicos, como el movimiento de ondas y otros comportamientos periódicos. Esto se debe a su capacidad para modelar relaciones entre diferentes elementos de un sistema físico.

Uso en geometría

En geometría, la función cosecante facilita la determinación de longitudes y distancias cuando se conocen ciertos ángulos. Esto amplía las posibilidades de cálculo y diseño en proyectos de construcción y diseño arquitectónico.

Características de la cosecante

Periodicidad y amplitud

Una característica fundamental de la función cosecante es su periodicidad. Es decir, sus valores se repiten a intervalos regulares, lo que se manifiesta gráficamente en sus repetitivos arcos. Además, su amplitud, o rango de valores, abarca desde el infinito negativo hasta el infinito positivo, pasando por puntos de no definición correspondientes a los ceros del seno.

Diferencias con otras funciones

Comparación con secante y cotangente

Aunque la cosecante, la secante y la cotangente son funciones recíprocas del seno, coseno y tangente respectivamente, cada una tiene sus propios gráficos y comportamientos. La diferencia principal radica en sus gráficas y en cómo se relacionan con el triángulo rectángulo. Mientras que la secante deriva del coseno y la cotangente de la tangente, la cosecante ofrece una perspectiva única al ser el recíproco del seno.

La función cosecante es un componente vital en el estudio y aplicación de la trigonometría. Aunque su mención puede ser menos frecuente que otras funciones trigonométricas, su comprensión y uso abren un abanico de posibilidades en diversos campos científicos y prácticos. Desde la modelación de fenómenos físicos hasta su aplicación en la resolución de problemas geométricos, la cosecante desempeña un papel irremplazable en el fascinante mundo de las matemáticas.

Video sobre Cosecante

Preguntas Frecuentes sobre Cosecante

¿Cómo calcular la cosecante?

Para calcular la cosecante (csc) de un ángulo en un triángulo rectángulo, primero necesitas determinar la longitud de la hipotenusa y del cateto opuesto a dicho ángulo. La fórmula para hallar la cosecante es (csc(theta) = frac{hipotenusa}{cateto opuesto}). Es importante tener en cuenta que la cosecante es el recíproco del seno, lo que implica que también se puede calcular como (csc(theta) = frac{1}{sen(theta)}). Este método de cálculo te permitirá entender cómo las proporciones y relaciones dentro de un triángulo rectángulo pueden ofrecer información sobre sus ángulos y lados, ampliando tu comprensión de la trigonometría.

¿En qué se diferencia la cosecante de otras funciones trigonométricas?

Las funciones trigonométricas como el seno, coseno, tangente, cotangente y secante, cada una destaca por representar distintas relaciones entre los ángulos y los lados de un triángulo rectángulo. La principal diferencia de la cosecante respecto a estas otras funciones es que se define como el recíproco del seno, es decir, mientras el seno representa la relación entre el cateto opuesto y la hipotenusa, la cosecante describe el vínculo inverso, entre la hipotenusa y el cateto opuesto. Esta peculiaridad le otorga un lugar único en el análisis y resolución de problemas trigonométricos, ofreciendo una perspectiva diferente para el estudio de las relaciones angulares.

¿Dónde se aplica la función cosecante en la vida real?

Las aplicaciones prácticas de la función cosecante se extienden a diversos campos como la ingeniería, la física, la arquitectura y las ciencias computacionales. Por ejemplo, en la ingeniería, se utiliza para calcular la longitud de ciertos componentes al conocer un ángulo y la longitud de un lado opuesto. En la física, facilita el análisis de ondas y vibraciones al emplear sus propiedades en el estudio de modelos oscilatorios. En las ciencias de la computación, la cosecante juega un papel fundamental en la generación de gráficos tridimensionales y en la resolución de problemas de geometría y posicionamiento. Estos usos demuestran cómo una función matemática puede tener aplicaciones concretas y valiosas en el mundo real.

¿Cómo ayuda entender la cosecante para resolver problemas geométricos?

Entender la función cosecante es fundamental en la resolución de problemas geométricos, especialmente cuando estos involucran triángulos rectángulos y la necesidad de hallar longitudes desconocidas. Con un conocimiento sólido de cómo la cosecante relaciona la hipotenusa con el cateto opuesto, es posible determinar dimensiones que de otro modo serían inciertas. Esto se aplica no solo en la teoría, sino también en situaciones prácticas que requieren precisión y comprensión de las propiedades geométricas, permitiendo un enfoque más eficaz y exacto en el análisis y diseño de estructuras, mecanismos o en la interpretación de fenómenos físicos.

¿Cuál es la importancia de la cosecante en trigonometría?

La importancia de la cosecante en trigonometría radica en su capacidad para complementar y proporcionar una perspectiva alternativa a la comprensión de las relaciones angulares y lineales en un triángulo. Al ser el recíproco del seno, la cosecante facilita la exploración de propiedades y resultados que pueden ser menos evidentes al trabajar exclusivamente con funciones más comunes como el seno o el coseno. Este enfoque ampliado es crucial para el desarrollo de técnicas analíticas avanzadas en matemáticas, física y en la ingeniería, haciendo de la cosecante una herramienta valiosa para los profesionales y estudiantes que buscan profundizar su conocimiento y resolver problemas complejos con mayor eficacia.

Si quieres conocer otros artículos parecidos a Cosecante: Definición, Función y Concepto en Matemáticas puedes visitar la categoría CIENCIAS.