
Qué es y qué propiedades tiene la función exponencial
- Una función exponencial, fundamental en la matemática, es la representación de fenómenos de crecimiento o decrecimiento acelerados, utilizando la fórmula f(x) = aˣ, con 'a' como base y 'x' como exponente.
- Además de su papel esencial en el modelado de situaciones como el aumento poblacional o el cálculo de intereses compuestos en finanzas, estas funciones destacan por sus interesantes propiedades, tales como tasas de cambio constantes y patrones de crecimiento/decrecimiento específicos.
- Desde el análisis de funciones con base natural 'e' hasta aquellas con bases arbitrarias, pasando por su vital relación con los logaritmos, las funciones exponenciales despliegan una riqueza de aplicación y teoría, incluyendo representaciones gráficas donde inflexiones y asíntotas juegan un papel clave, así como métodos para resolver ecuaciones exponenciales.
Las funciones exponenciales representan uno de los conceptos más fascinantes y poderosos en el mundo de las matemáticas. Estas no solo capturan la esencia de fenómenos en crecimiento acelerado sino que también ofrecen herramientas para modelar con precisión una amplia gama de procesos en la ciencia, la economía y más allá.
Nos sumergiremos profundamente en el universo de la función exponencial, explorando su definición, propiedades fundamentales, aplicaciones prácticas y mucho más. Prepárate para un viaje por la increíble versatilidad y el poder transformador de estas funciones.
Definición de función exponencial
En términos simples, una función exponencial se define como cualquier función matemática de la forma (f(x) = a^x), donde (a) es la base, un número real positivo distinto de 1, y (x) es el exponente, que puede tomar cualquier valor real. Este tipo de función destaca por su capacidad de modelar crecimiento y decrecimiento exponenciales, características que la hacen invaluable en múltiples campos.
Base y exponente en estas funciones
La base (a) y el exponente (x) juegan roles cruciales en una función exponencial. Mientras la base determina la tasa de crecimiento o decrecimiento, el exponente representa la variable dependiente cuya variación afecta directamente el valor de la función. Es esta interacción entre base y exponente la que confiere a las funciones exponenciales su notable flexibilidad y aplicabilidad.
Propiedades fundamentales
Crecimiento y decrecimiento
Una de las características más impresionantes de las funciones exponenciales es su capacidad para describir tanto procesos de crecimiento exponencial como de decrecimiento exponencial. Este comportamiento depende íntegramente de la base de la función: si la base es mayor que 1, observaremos un crecimiento exponencial; si es menor que 1 (pero mayor que 0), la función reflejará un decrecimiento exponencial.
Tasa de cambio constante
Las funciones exponenciales también destacan por tener una tasa de cambio proporcional a su propia magnitud. Esto significa que, a medida que el valor de la función aumenta o disminuye, la velocidad de este cambio también lo hace en proporción directa. Tal propiedad es clave para entender el rápido crecimiento o decrecimiento que estas funciones pueden modelar.
Aplicaciones prácticas
Modelado de poblaciones
En la biología y la ecología, las funciones exponenciales son esenciales para modelar el crecimiento poblacional. Estas permiten a los científicos predecir cómo se desarrollarán las poblaciones de seres vivos bajo condiciones ideales, mostrando patrones de crecimiento que son fundamentales para planificar y administrar recursos.
Intereses compuestos en finanzas
El mundo de las finanzas también se beneficia enormemente de las funciones exponenciales mediante el cálculo de intereses compuestos. Aquí, la capacidad de modelar cómo el interés generado sobre una inversión se suma al capital original, creando un ciclo de crecimiento exponencial del capital total, es fundamental para la comprensión de inversiones y ahorros a largo plazo.
Tipos de funciones exponenciales
Función de base natural e
Entre las diversas funciones exponenciales, la función de base natural (e) (aproximadamente 2.718) ocupa un lugar especial. Esta base proporciona una particularidad matemática única, ya que la tasa de cambio de la función exponencial (e^x) es igual a su propio valor. Su omnipresencia en el cálculo y en el modelado de procesos naturales la hacen de invaluable importancia.
Funciones de base arbitraria
Además de la base natural, las funciones exponenciales pueden construirse con cualquier base positiva y real distinta de 1. Estas funciones de base arbitraria se ajustan a necesidades específicas de modelado en diversas disciplinas, desde la física hasta la economía, permitiendo una adaptación precisa a los fenómenos estudiados.
Representación gráfica
Inflexión y asíntotas
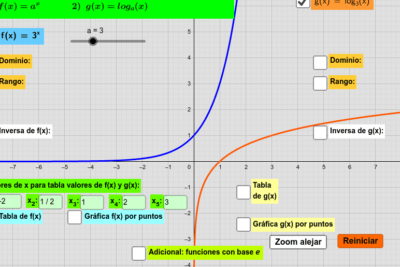
La representación gráfica de una función exponencial revela características clave como puntos de inflexión, donde la curvatura de la gráfica cambia, y asíntotas, líneas que la gráfica se acerca indefinidamente sin llegar a tocar. Entender estos elementos es crucial para visualizar y comprender el comportamiento de las funciones exponenciales.
Ecuaciones exponenciales
Resolución de ecuaciones básicas
Las ecuaciones exponenciales, en las que la variable desconocida aparece como exponente, plantean desafíos únicos. Sin embargo, métodos como la igualación de bases y el uso de logaritmos permiten solucionar estas ecuaciones de forma efectiva, abriendo las puertas a una comprensión más profunda de las dinámicas que describen.
Relación con logaritmos
Logaritmo como inversa
Los logaritmos juegan un papel fundamental en la manipulación de las funciones exponenciales, actuando como su función inversa. Esta relación permite transformar multiplicaciones en sumas, potencias en productos y ecuaciones exponenciales en formas lineales, facilitando su análisis y resolución. Además, subraya la interconexión matemática entre distintos tipos de funciones y operaciones.
Conclusión
Las funciones exponenciales emergen como uno de los pilares de las matemáticas modernas, con una profundidad y aplicabilidad que trascienden disciplinas y campos de estudio. Desde su definición y propiedades hasta su interrelación con los logaritmos, estas funciones despliegan un universo de posibilidades para modelar, analizar y comprender el mundo que nos rodea de maneras cada vez más precisas y significativas.
Video Relacionado sobre Funcion Exponencial
FAQ Acerca de Funcion Exponencial
¿Qué es una función exponencial?
Una función exponencial es una expresión matemática clave que se manifiesta en múltiples contextos, desde el crecimiento de poblaciones hasta el interés compuesto en finanzas. Su principal característica es que la variable independiente figura como exponente en la potencia de una base constante. Este aspecto único conduce a un crecimiento o decrecimiento que no es lineal, sino exponencial. La estructura general de esta función se resume en la fórmula f(x) = a^x, donde 'a' es una constante positiva distinta de 1, e 'x' representa la variable independiente.
La función exponencial tiene la particularidad de que su tasa de cambio es directamente proporcional a su valor actual. Esto significa que mientras mayor sea el valor de la función, mayor será su tasa de crecimiento, configurando una curva de crecimiento acelerado en el gráfico. Dicho comportamiento es crucial para modelar procesos naturales y financieros donde el cambio ocurre a un ritmo que depende del estado actual.
Es importante resaltar que todas las funciones exponenciales pasan por el punto (0, 1) en el plano cartesiano, independientemente del valor de 'a'. Además, estas funciones nunca alcanzan el valor 0, tendiendo hacia él pero sin llegar en el caso de crecimientos, y alejándose infinitamente en el caso de decrecimientos. Este comportamiento refleja la naturaleza persistente y perpetua del crecimiento exponencial en el ámbito teórico y real.
¿Cuáles son las propiedades principales de la función exponencial?
Las funciones exponenciales se distinguen por un conjunto de propiedades que las hacen útiles y predecibles en diversos campos del conocimiento. Algunas de estas propiedades son:
1. **Dominio y Rango**: El dominio de una función exponencial incluye todos los números reales, mientras que el rango se compone únicamente de números reales positivos. Esto se debe a que, matemáticamente, no existe un número real que elevado a otra cifra resulte en un número negativo o en cero cuando hablamos de bases positivas reales.
2. **Crecimiento y Decrecimiento**: Dependiendo del valor de la base 'a', la función puede representar un crecimiento o un decrecimiento exponencial. Si 0 < a < 1, la función muestra un decrecimiento exponencial; si a > 1, se observa un crecimiento exponencial. Este cambio radical en el comportamiento subraya la sensibilidad de la función a los valores de su base.
3. **Intersección en el eje Y**: Independientemente de la base 'a', todas las funciones exponenciales cruzan el eje Y en el punto (0,1), demostrando que cualquier número elevado a 0 resulta en 1. Este punto de intersección es fundamental para entender cómo se estructuran estas funciones en un plano cartesiano.
4. **Asíntota Horizontal**: Las funciones exponenciales tienen una asíntota horizontal en y = 0. Esto significa que la curva de la función se acerca infinitamente al eje X sin tocarlo ni cruzarlo. Esta propiedad refleja el decrecimiento infinito de la función hacia el eje X mientras x tiende a valores negativos infinitamente grandes.
5. **Continuidad y Diferenciabilidad**: Las funciones exponenciales son continuas y diferenciables en todo su dominio. Esto implica que no presentan saltos, huecos, ni discontinuidades, y que su tasa de cambio puede calcularse en cualquier punto. Estas propiedades son cruciales para el análisis y la modelización de fenómenos reales utilizando funciones exponenciales.
Por último, el impacto y la aplicación de las funciones exponenciales se extienden más allá de las matemáticas, influyendo en ámbitos como la biología, la economía y la física, lo que demuestra su relevancia y versatilidad.
Si quieres conocer otros artículos parecidos a Qué es y qué propiedades tiene la función exponencial puedes visitar la categoría MATEMÁTICAS.
Deja una respuesta



También te puede interesar: